前言

終於結束了安全性演算法的部分，有興趣的人可以進一步學習密碼學，筆者想推薦一個課程：

Udemy：數論與密碼學 (Python, JavaScript)

課程講解得很清楚，老師將複雜的觀念分解為各個小議題進行教學，若是喜歡這個老師的課程，也可以選修其他的課程，支持認真開課的老師，大家一起讓學習環境變得更好吧！

河內塔(Tower of Hanoi)

Hanoi是越南的首都，筆者曾經在越南旅行了一個月，尤其非常喜歡Hanoi這個地方。推薦一個到Hanoi必喝的飲料，「椰子冰沙咖啡」，為這個因為疫情暫時不能旅行的時期，提供一點不一樣的能量。

河內塔(Tower of Hanoi)是移動圓盤的遊戲，可以幫助輕鬆理解遞迴演算法(recursive algorithm)。先來看看河內塔是什麼：

執行次數：
假設解n個圓盤的河內塔，執行次數為T(n)，一個圓盤用一步就結束了，所以T(n)=1，n個圓盤時，首先要將上面的n-1個圓盤從A移動到B，為T(n-1)步，把最大的圓盤移動到C是一步，把位在B的n-1個圓盤移動到C是T(n-1)步，所以T(n)=2T(n-1)+1，可得T(n)=(2**n)-1，執行次數比這個還少的解法並不存在

Python

def hanoi(n, A, B, C):
    if n == 1:
        print(f"{A}->{C}")
    else:
        hanoi(n-1, A, C, B) 
        hanoi(1, A, B, C) 
        hanoi(n-1, B, A, C)

n = int(input())
hanoi(int(n), 'A', 'B', 'C')

JavaScript

function towerOfHanoi(n , start , target ,buffer){

    if(n>0){
        towerOfHanoi(n-1, start, buffer, target); 
        target.push(start.pop());   
        towerOfHanoi(n-1, buffer, target, start); 
    }
}

遞迴演算法(recursive algorithm)

遞迴演算法(recursive algorithm)是重複將問題分解為同類的子問題來解決問題的方法，可參考「合併排序」、「快速排序」。

遞迴的關鍵點在於這是一個「呼叫自己的函數」，這時候需要設置一個終止條件，將結果返回給呼叫者。

接下來看一個影片，影片內容是關於Python中的遞迴：

斐波那契數列(Fibonacci sequence)

Fibonacci sequence又稱為黃金分割數列，是數學家Leonardoda Fibonacci以兔子繁殖為例子，延伸出來的有趣理論。這個理論內容如下：

• 如果一對兔子每月能生一對小兔（一雄一雌），而每對小兔在牠出生後的第三個月裡，又能開始生一對小兔，假定在不發生死亡的情況下，由一對出生的小兔開始，50個月後會有多少對兔子？

• 第一個月時，只有一對小兔子，過了一個月，那對兔子成熟了，在第三個月時便生下一對小兔子，這時有兩對兔子。再過多一個月，成熟的兔子再生一對小兔子，而另一對小兔子長大，有三對小兔子。如此推算下去，我們便發現一個規律：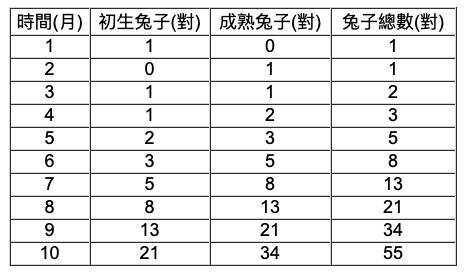
  

• 由此可知，從第一個月開始以後每個月的兔子總數是:
  1,1,2,3,5,8,13,21,34,55,89,144,233…

若把上述數列繼續寫下去，得到的數列便稱為斐波那契數列。